Start Machine learning with A-STAR algorithm
- Tech Stack:Python
- URL: Medium Article Link
Why choose to use the A-star algorithm :
1.Heuristics:
A* uses a heuristic function that estimates the cost of the cheapest path from the current node to the goal node. This heuristic helps the algorithm prioritize which nodes to explore first, making it more efficient than other algorithms that explore nodes randomly.
2.Flexibility:
The A* algorithm can be customized by changing the heuristic function to suit different applications and problem domains.
3.Optimality:
The A* algorithm guarantees that it will find the shortest path between a starting point and a goal point, provided certain conditions are met.
Intro Heuristic in A-star algorithm :
Heuristic Algorithm estimates the distance from a given node to the goal node in a search space. Heuristics are used to guide the A* algorithm in exploring the search space efficiently and finding the shortest path from a starting node to the goal node.
Various types of heuristics can be used with the A* algorithm, including Manhattan distance, Euclidean distance, and straight-line distance.
Manhattan distance
only moving up, down, right, and left 4 directions

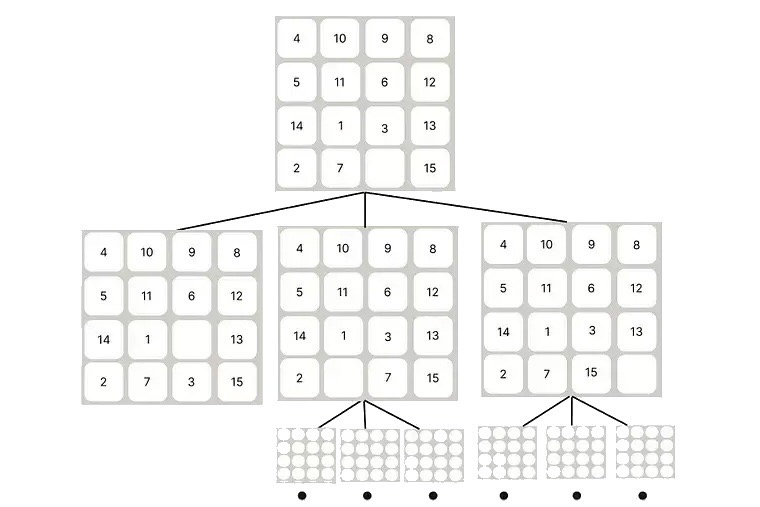
There are three moves that the blank can go.
calculate the after-state distance
If the blank goes up ->
h(x) = 3+5+3+3+0+1+3+1+4+2+2+1+4+2+1 = 35
If the blank goes right ->
h(x) =3+ 2+ 4+ 1+ 0+ 2+ 1+ 1+ 2+ 3+ 2+ 4+ 4+ 3 = 32
If the blank goes left ->
h(x) =3+ 2+ 4+ 1+ 0+ 2+ 1+ 1+ 2+ 3+ 2+ 4+ 4+ 3+ 1 = 32
Other kinds of Heuristic:
Euclidean distance
allows any direction of movement
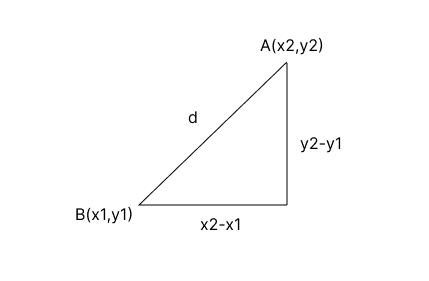
d =√[(x2-x1)2 + (y2-y1)2]
Euclidean distance
allows any direction of movement
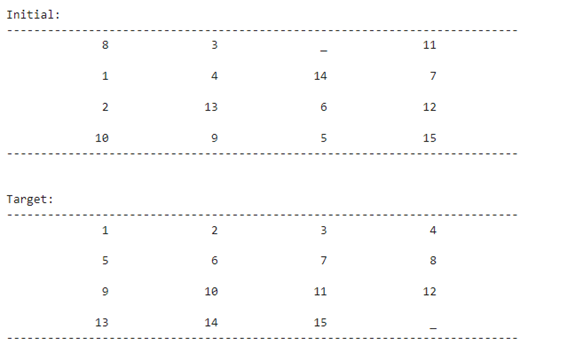
Now we know how Heuristics calculate, it's time for the A* algorithm!
How does the A-star Algorithm works
Steps in the Algorithm:
1.Initialize the starting node with a cost of zero and add it to an open set. The open set contains nodes that are yet to be evaluated.
2.While the open set is not empty, select the node with the lowest cost from the open set. This node will be the current node.
3.If the current node is the goal node, the algorithm terminates and returns the optimal path. Otherwise, generate all the neighbor nodes of the current node and calculate their cost using a combination of the actual cost from the starting node to the neighbor node and an estimated cost from the neighbor node to the goal node using a heuristic function.
4.For each neighbor node, if it is not in the open set or the cost to reach it is lower than the previously calculated cost, update its cost and set its parent to the current node. Add the neighbor node to the open set.
5.Repeat steps 2–4 until the goal node is found or the open set is empty.
Heuristic I'm using in this project :
h1 = the number of Misplaced tiles
h2 = the Manhattan distance
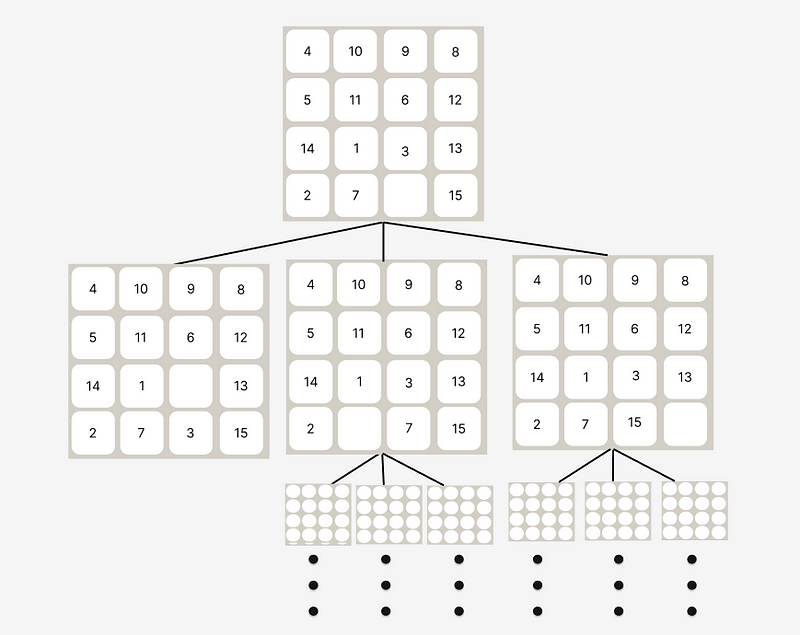
Regarding the priority, the computer will choose to keep generating child nodes on the lower f(x), from the example above it will generate another 4 direction nodes on the after-state of moving blank right and left.
The diagram will be like this :
Result :
In this project, I implemented two different heuristics: h1 and h2. h1 heuristics measure the number of tiles misplaced in the puzzle, while h2 heuristics calculate the total Manhattan distance, which is the sum of the horizontal and vertical distance between the current position of each tile and its target position. h1 and h2 heuristics have a search cost that determines the number of nodes to expand in the search process to find a solution.
The A* algorithm works by iteratively selecting the node with the lowest total cost from the open list, generating its sub-nodes, and adding them to the open list, and I use functions to calculate its total cost.
Finally, the algorithm stops when the target state is reached or when there are no more nodes to explore.
The A* algorithm iteratively selects the node with the lowest total cost from list(open) and generates its sub-nodes. The algorithm then uses the "f " function to calculate the total cost of each sub-node and the h function to calculate the numbers that are not in the right place and add them to the list. The cycle continues until the target state is reached. Finally, the code prints out the solution by tracing the path from the target node to the initial node.
However, it is worth noting that the search cost for both heuristics varies depending on the initial state of the puzzle. For example, some starting states may require more nodes to expand than others. In addition, the performance of the A* algorithm depends on the data structure used for storage. In my implementation, I used Python's built-in list data structure, but I have observed people on the site using a priority queue data structure, which may yield better performance results.
h1: f = misplaced + the distance from start to n
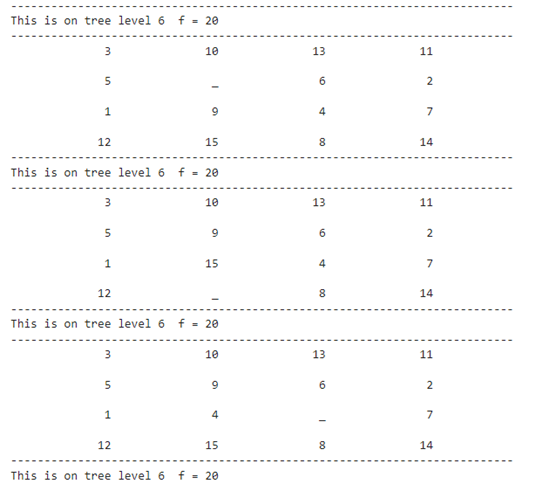
h2: f = total Manhattan distance+ the distance from start to n

Analysis of the result :
The total Manhattan distance heuristic(h2) is usually less costly than the misplaced tiles heuristic(h1). This is because the Manhattan distance provides a better estimate of the actual distance between the current state and the resulting state, whereas a misplaced number of misplaced tiles can be misleading and may lead to a suboptimal solution.
According to a University of Washington slide show, a tested 8-puzzle A*h1 of the same depth generates many more nodes than A*h2, so it is clear that in general h2's performance is better than that of h1.

References :
Problem Solving using Search. CSEP573: Artificial intelligence. (n.d.). Retrieved March 30, 2023, from https://courses.cs.washington.edu/courses/csep573/
Patel, A. (n.d.). A*'s Use of the Heuristic. Amit's A* Pages. Retrieved March 30, 2023, from http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html